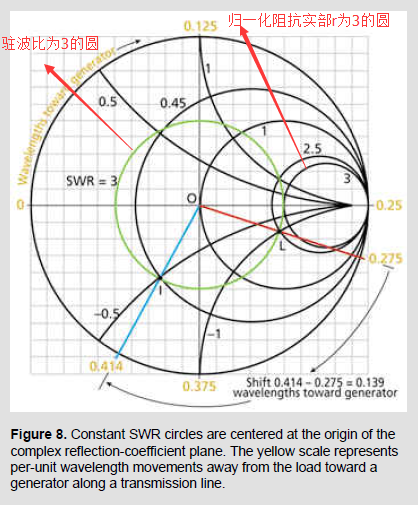
史密斯圆介绍
史密斯圆图是三张图画在一个坐标系上。 这个坐标系的x轴是电压反射系数的实部,y轴是电压反射系数的虚部。第一张图是等反射系数圆图,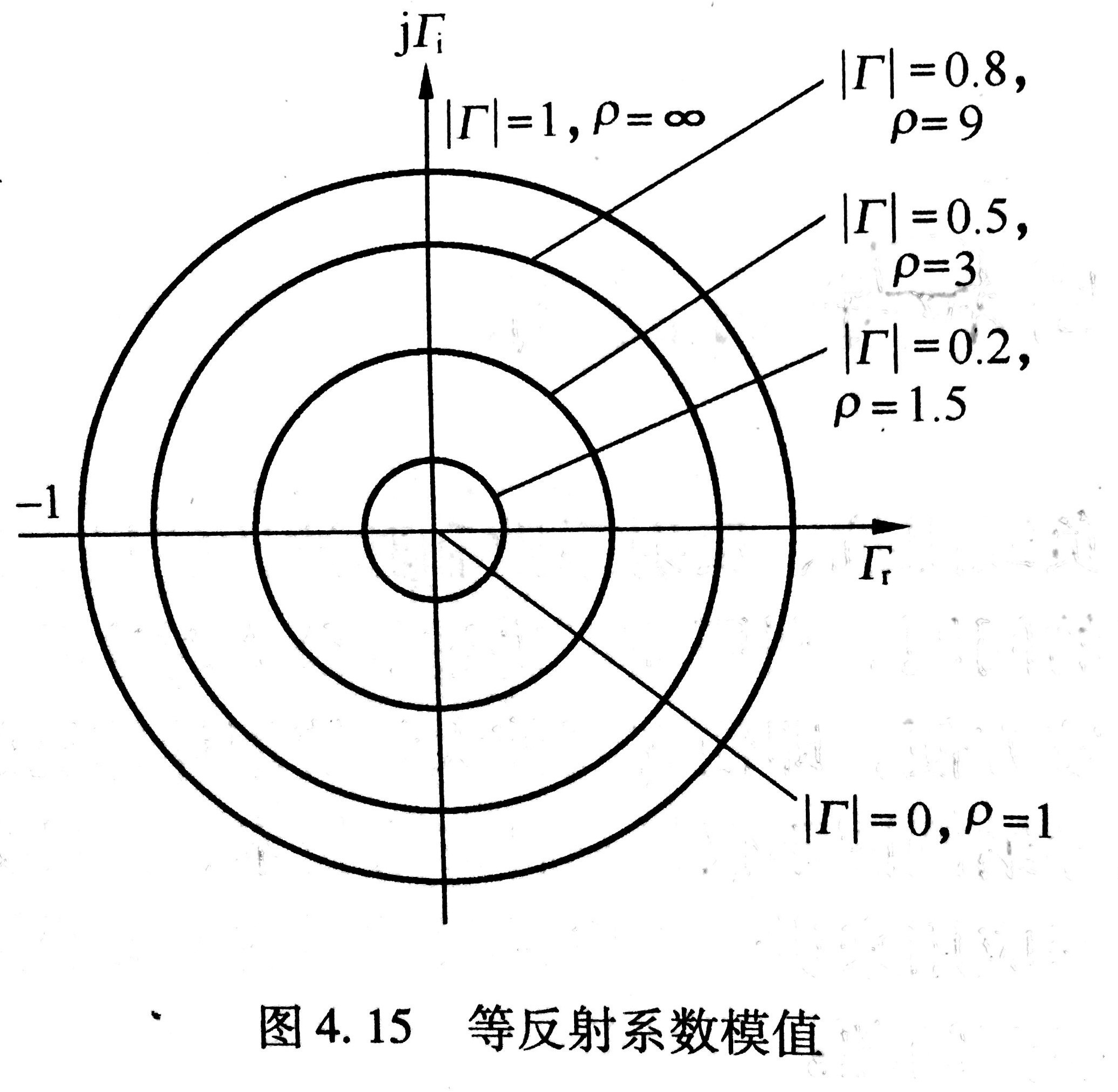
第二张是归一化等电阻圆图,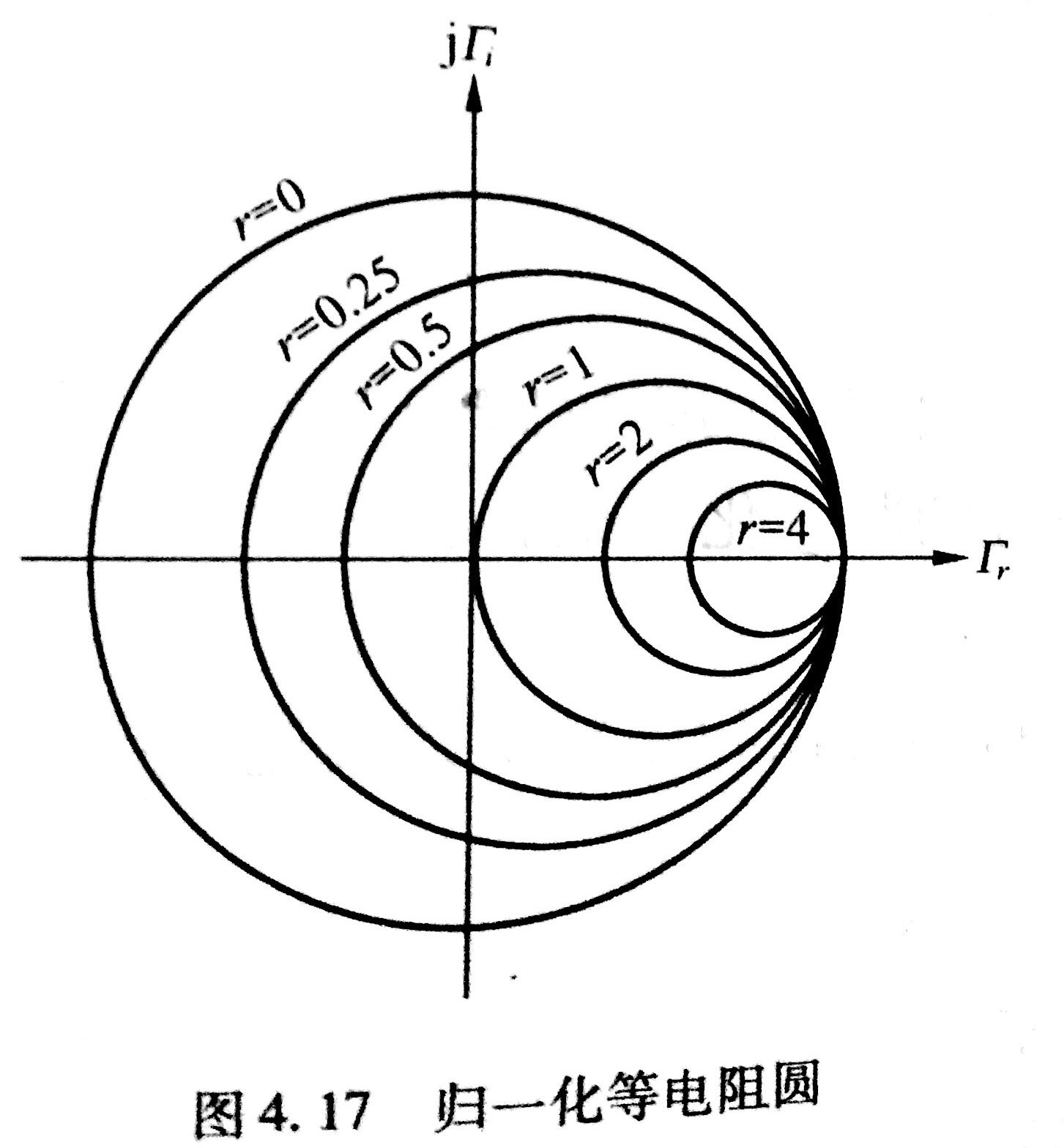
第三张是等电抗圆图。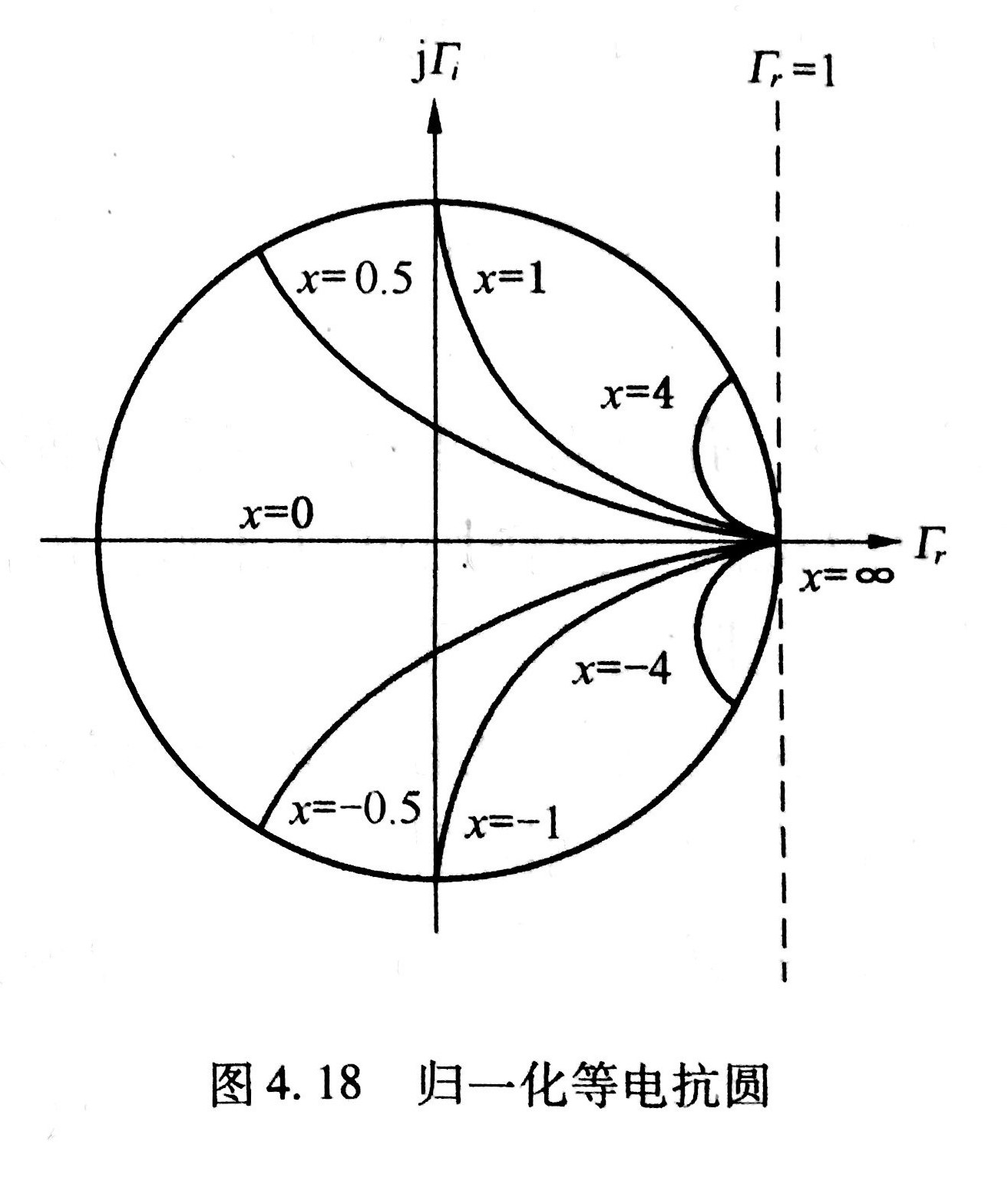
这三张图正好用的是同一个坐标系,直接把这三张图叠在一起,再取等反射系数圆图中反射系数为1的圆内部的交集即为史密斯圆图(因为等反射系数圆图中,反射系数最大是1,反射系数为1的圆以外的区域是没有物理意义的)。最后的史密斯圆图内的等反射系数圆图不画出来,只标注了角度变化,远离负载为顺时针旋转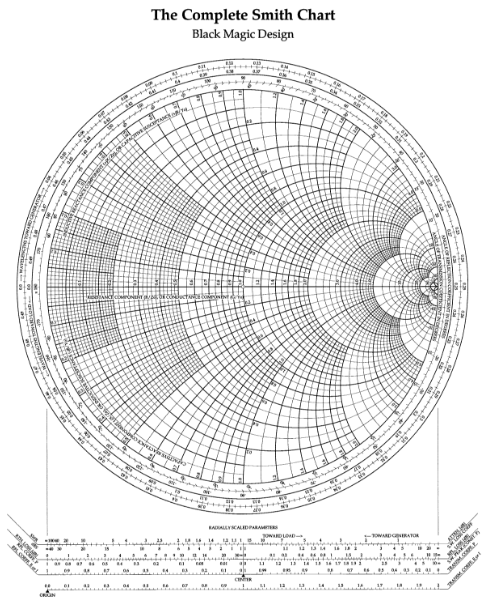
驻波比计算步骤
1.确定归一化阻抗在史密斯圆图中的位置,如A;
2.过A点,以坐标原点为圆心作圆(即作过A点的等反射系数圆图),圆交x正半轴与点B;
3.找到归一化等电阻圆图中过B点的圆,其阻抗实部(电阻)的值为r;
4.该传输线上的驻波比的值即为r;
为什么这么计算
在黄玉兰编著的《电磁场与微波技术》一书中这样解释道
圆图上实轴是x=0的轨迹,其中正实半轴为电压波腹点的轨迹,线上r的读即为驻波比的读数
我一直没明白这句话的意思。但自己试着从书中的公式推导,可以得到上述的结论。先看归一化等电阻圆图的方程:
$ (\Gamma_r-{r\over 1+r})^2+\Gamma_i^2=({1\over 1+r})^2$
当归一化等电阻圆交于x轴时,$\Gamma_i$=0,所以
$\Gamma_r={r-1\over r+1}$或1
则B坐标为(${r-1\over r+1}$,0)
而当等反射系数圆图也经过B点时,反射系数$$|\Gamma|=|\Gamma_r+j\Gamma_i|=|{r-1\over r+1}|={r-1\over r+1}$$(x正半轴r>=1)
而驻波比的方程为
$\rho={1+|\Gamma| \over 1-|\Gamma| }$
带入可得
$\rho=r$
上述结论用图形化语言表述可以更直观,那就是“在史密斯圆图中,与等反射系数圆相切的归一化等电阻圆的电阻值就等于该等反射系数圆的驻波比值。”